☛ Intersection des hauteurs d'un triangle

Énoncé

Soit \(\text{ABC}\) un triangle. On note : 

• \(h_\text{A}\) la hauteur issue de \(\text{A}\) ;
  
• \(\text{A}'\) le point d'intersection des droites \(h_\text{A}\) et \((\text{BC})\) ;
  
• \(h_\text{B}\) la hauteur issue de \(\text{B}\) ;
  
• \(\text{B}'\) le point d'intersection des droites \(h_\text{B}\) et \((\text{AC})\) ;
  
• \(h_\text{C}\) la hauteur issue de \(\text{C}\) ;
  
• \(\text{C}'\) le point d'intersection des droites \(h_\text{C}\) et \((\text{AB})\).
  

On admet que les trois médiatrices d'un triangle sont concourantes en un point appelé centre du cercle circonscrit au triangle.

1. Faire une figure représentant la situation de l'énoncé.

2. a. Construire la droite \(d_1\) parallèle à la droite \((\text{BC})\) et passant par le point \(\text{A}\).
    b. Construire la droite \(d_2\) parallèle à la droite \((\text{AC})\) et passant par le point \(\text{B}\).
    c. Construire la droite \(d_3\) parallèle à la droite \((\text{AB})\) et passant par le point \(\text{C}\).
On note :

• \(\text{D}\) le point d'intersection des droites \(d_1\) et \(d_2\) ;
  
• \(\text E\) le point d'intersection des droites \(d_1\) et \(d_3\) ;
  
• \(\text{F}\) le point d'intersection des droites \(d_2\) et \(d_3\).
  

3. a. Démontrer que le quadrilatère \(\text{ACBD}\) est un parallélogramme.
    b. Démontrer que le quadrilatère \(\text{ABCE}\) est un parallélogramme.
    c. En déduire que \(\overrightarrow{\text{DA}} = \overrightarrow{\text{AE}}\). Que peut-on en déduire pour le point \(\text{A}\) ?
    d. Que représente la droite \((\text{AA}')\) pour le segment \([\text{DE}]\) ?

4. De façon analogue, démontrer que la droite \((\text{BB}')\) est la médiatrice du segment \([\text{DF}]\).

5. On admet que l'on démontre de même que la droite \((\text{CC}')\) est la médiatrice du segment
\([\text{EF}]\). Démontrer alors que les trois hauteurs \(h_\text{A}, h_\text{B}\) et \(h_\text{C}\) sont concourantes en un point.
Ce point est appelé orthocentre du triangle \(\text{ABC}\).

Solution

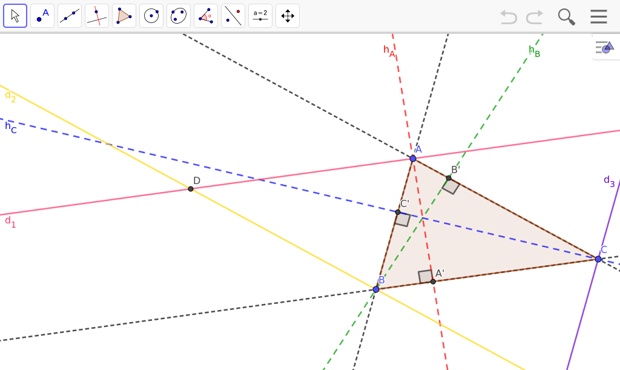
Questions 1. et 2. 

3. a. Par construction, les droites \((\text{AC})\) et \((\text{BD})\) sont parallèles. De même, les droites \((\text{BC})\) et \((\text{AD})\) sont parallèles. On en déduit que les côtés opposés du quadrilatère \(\text{ACBD}\) sont parallèles deux à deux. Donc \(\text{ACBD}\) est un parallélogramme.
    b. De même, les droites \((\text{AB})\) et \((\text{CE})\) sont parallèles, et les droites \((\text{AE})\) et \((\text{BC})\) sont parallèles. Donc \(\text{ABCE}\) est un parallélogramme.
    c. D'après la question 3. a., \(\text{ACBD}\) est un parallélogramme donc \(\overrightarrow{\text{BC}}=\overrightarrow{\text{DA}}\).
        Et d'après la question 3. b., \(\text{ABCE}\) est un parallélogramme, donc  \(\overrightarrow{\text{BC}}=\overrightarrow{\text{AE}}\).
        Donc \(\overrightarrow{\text{DA}}=\overrightarrow{\text{AE}}\).
        On en déduit que \(\text{A}\) est le milieu de \([\text{DE}]\).
    d. \((\text{AA}')\) est perpendiculaire à \((\text{BC})\) et \((\text{BC})\) est parallèle à \((d_1)\), c'est-à-dire \((\text{DE})\). Donc \((\text{AA}')\) est perpendiculaire à \((\text{DE})\) et passe par \(\text{A}\), le milieu de \([\text{DE}]\).
On en déduit que \((\text{AA}')\) est la médiatrice de  \([\text{DE}]\).

4. D'après la question précédente, on sait que \(\text{ACBD}\) est un parallélogramme et donc que  \(\overrightarrow{\text{DB}}=\overrightarrow{\text{AC}}\).
Par construction, les droites \((\text{AC})\) et \((\text{BF})\) sont parallèles ; de même, les droites \((\text{AB})\) et \((\text{CF})\) sont parallèles. Ainsi \(\text{ACFB}\) est un parallélogramme. Donc \(\overrightarrow{\text{AC}}=\overrightarrow{\text{BF}}\).
On en déduit que \(\overrightarrow{\text{DB}}=\overrightarrow{\text{BF}}\), d'où \(\text{B}\) est le milieu de \([\text{DF}]\).
\((\text{BB}')\) est perpendiculaire à \((\text{AC})\) et \((\text{AC})\) est parallèle à \((d_2)\), c'est-à-dire \((\text{DF})\). Donc \((\text{BB}')\) est perpendiculaire à \((\text{DF})\) et passe par \(\text{B}\), le milieu de \([\text{DF}]\).
On en déduit que \((\text{BB}')\) est la médiatrice de \([\text{DF}]\).

5. D'après les questions précédente, on a donc :

• la droite \((\text{AA}')\), c'est-à-dire la droite \(h_\text{A}\), est la médiatrice de \([\text{DE}]\) ;
  
• la droite \((\text{BB}')\), c'est-à-dire la droite \(h_\text{B}\), est la médiatrice de \([\text{DF}]\) ;
• la droite \((\text{CC}')\), c'est-à-dire la droite \(h_\text{C}\), est la médiatrice de \([\text{EF}]\) ;
• les points \(\text{D}, \text{E}\) et \(\text{F}\) ne sont pas alignés par construction, donc ils forment un triangle.
  

Or, les trois médiatrices d'un triangle sont concourantes.
Donc les trois médiatrices \(h_\text{A}, h_\text{B}\) et \(h_\text{C}\) du triangle \(\text{DEF}\) sont concourantes.
On a bien démontré que les trois hauteurs \(h_\text{A}, h_\text{B}\) et \(h_\text{C}\) du triangle \(\text{ABC}\) sont concourantes.